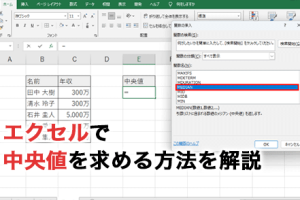
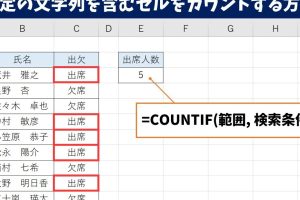
Excelカイ二乗検定で統計分析を簡単に

Excelのカイ二乗検定は、統計分析を簡単に行うための強力なツールです。この検定は、2つのカテゴリ変数間の関連性を調べるために使用され、データ分析の基本的な手法となっています。カイ二乗検定を用いると、観察されたデータが偶然によるものなのか、あるいは有意な関連があるのかを判断できます。Excelでは、この検定を簡単に行うことができ、データの傾向を把握するのに役立ちます。カイ二乗検定の基本とExcelでの実行方法を理解しましょう。データ分析の精度を高め、ビジネスや研究に役立てましょう。

Excelを使ったカイ二乗検定の基本的な手順

Excelのカイ二乗検定機能を使用することで、統計分析が簡単に実行できます。カイ二乗検定は、2つのカテゴリ変数間の関連性を調べるために使用される統計的手法です。例えば、性別と製品の購入傾向の間に有意な関連があるかどうかを調べることができます。

カイ二乗検定の前提条件

カイ二乗検定を実行する前に、いくつかの前提条件を確認する必要があります。

1. データのカテゴリ化：データはカテゴリ変数である必要があります。例えば、性別（男性/女性）、製品の購入（あり/なし）などです。
2. データの独立性：各観測値は独立している必要があります。つまり、一つの観測値が他の観測値に影響を与えないことを意味します。
3. 期待度数の確認：各カテゴリの期待度数が5以上であることが推奨されます。

Excelでのカイ二乗検定の実行方法

Excelでカイ二乗検定を実行するには、次の手順に従います。

1. データの準備：分析するデータをExcelのワークシートに準備します。データは、カテゴリ変数ごとに列または行にまとめられている必要があります。
2. ピボットテーブルの作成：ピボットテーブルを使用して、カテゴリ変数ごとの度数を集計します。
3. カイ二乗検定の実行：Excelの関数（例：CHISQ.TEST）を使用して、カイ二乗検定を実行します。

カイ二乗検定の結果の解釈

カイ二乗検定の結果は、p値によって解釈されます。

1. p値の確認：p値が有意水準（通常は0.05）より小さい場合、帰無仮説（2つの変数間に関連性がない）を棄却し、2つの変数間に関連性があると結論付けます。
2. 関連性の方向：カイ二乗検定は、関連性の方向までは示しません。関連性の方向を知るには、さらに分析が必要です。

カイ二乗検定の限界

カイ二乗検定にはいくつかの限界があります。

1. カテゴリ数：カテゴリの数が多い場合、カイ二乗検定の結果の解釈が難しくなることがあります。
2. サンプルサイズ：サンプルサイズが小さい場合、カイ二乗検定の結果が不正確になることがあります。

Excelカイ二乗検定の応用例

Excelのカイ二乗検定は、さまざまな分野で応用できます。

1. マーケティング分析：顧客の属性と購買行動の関連性を分析する際に使用できます。
2. 医学研究：疾患の有無と特定の要因（例えば、喫煙習慣）との関連性を調べるために使用できます。

エクセルでのカイ二乗検定のやり方は？

エクセルでのカイ二乗検定は、観測されたデータが期待される分布に従っているかどうかを検証するために用いられる統計的手法です。この検定は、カテゴリデータの分析に広く利用されています。まず、データを適切に整理する必要があります。具体的には、観測された頻度と期待される頻度を別々の列または行にまとめます。次に、エクセルの関数を利用してカイ二乗統計量を計算します。カイ二乗統計量は、観測された頻度と期待される頻度の差に基づいて計算されます。

カイ二乗検定の基本的な手順

カイ二乗検定を実行するには、まずデータの準備が必要です。観測データと期待データの両方を用意し、エクセルのワークシートに整理します。次に、カイ二乗統計量を計算するために、エクセルのCHISQ.TEST関数またはCHISQ.DIST.RT関数を使用します。これらの関数を使うことで、カイ二乗検定のp値を算出できます。p値が一定の有意水準（通常は0.05）より小さい場合、帰無仮説は棄却されます。

1. データの準備：観測された頻度と期待される頻度を整理します。
2. カイ二乗統計量の計算：エクセルの関数を利用してカイ二乗統計量を算出します。
3. p値の解釈：p値を有意水準と比較して帰無仮説を検証します。

エクセルでのカイ二乗検定の実行方法

エクセルでカイ二乗検定を実行するには、具体的にはCHISQ.TEST関数を使用します。この関数は、観測された頻度と期待される頻度の範囲を指定することで、カイ二乗検定のp値を直接算出します。データ範囲を正確に指定することが重要です。また、エクセルのバージョンによっては、分析ツールのアドインを有効にする必要がある場合があります。

1. CHISQ.TEST関数の使用：観測データと期待データの範囲を指定してp値を計算します。
2. 分析ツールの有効化：必要に応じて、エクセルの分析ツールを有効にします。
3. 結果の解釈：得られたp値を基に、統計的な有意性を判断します。

カイ二乗検定の結果の解釈

カイ二乗検定の結果は、p値に基づいて解釈されます。p値が有意水準（通常0.05）より小さければ、帰無仮説（観測データが期待される分布に従っている）を棄却し、観測データは期待される分布に従っていないと結論付けられます。逆に、p値が有意水準より大きければ、帰無仮説を棄却できず、観測データは期待される分布に従っている可能性が高いと判断されます。

1. p値の比較：p値を有意水準と比較します。
2. 帰無仮説の検証：p値に基づいて帰無仮説を棄却するかどうか判断します。
3. 結果の報告：検定の結果を適切に報告します。

カイ二乗検定で分かることは何ですか？

カイ二乗検定は、観測データと期待度数の差を評価するために使用される統計的手法です。この検定により、2つのカテゴリ変数間に有意な関連性があるかどうかを判断できます。カイ二乗検定の結果は、観測された分布が偶然によるものか、または何らかの要因によるものかを判断するのに役立ちます。

カイ二乗検定の基本的な考え方

カイ二乗検定の基本的な考え方は、観測度数と期待度数を比較することです。期待度数は、特定の仮説（通常は「2つの変数は独立している」という仮説）に基づいて計算されます。カイ二乗統計量は、これらの差の二乗の合計を期待度数で割った値です。カイ二乗検定の主な利点は以下の通りです。

1. 独立性の検定に使用できる
2. 適合度の検定にも使用できる
3. 多様なデータに対応できる

カイ二乗検定の適用例

カイ二乗検定は、さまざまな分野で使用されています。たとえば、医学研究では、治療法と患者の回復率の関係を分析するために使用されます。また、市場調査では、消費者の嗜好と人口統計学的特徴の関係を分析するために使用されます。カイ二乗検定の適用例には以下のようなものがあります。

1. 臨床試験での治療効果の評価
2. アンケート調査の結果分析
3. 品質管理での不良品の発生率分析

カイ二乗検定の解釈

カイ二乗検定の結果を解釈する際には、p値に注目します。p値が有意水準（通常は0.05）より小さい場合、帰無仮説（2つの変数は独立している）を棄却し、2つの変数間に関連があると結論付けます。また、カイ二乗統計量の値が大きいほど、観測度数と期待度数の差が大きいことを示します。カイ二乗検定の解釈のポイントは以下の通りです。

1. p値の大小による判断
2. カイ二乗統計量の値の解釈
3. 自由度の考慮

ExcelのT-testには何種類ありますか？

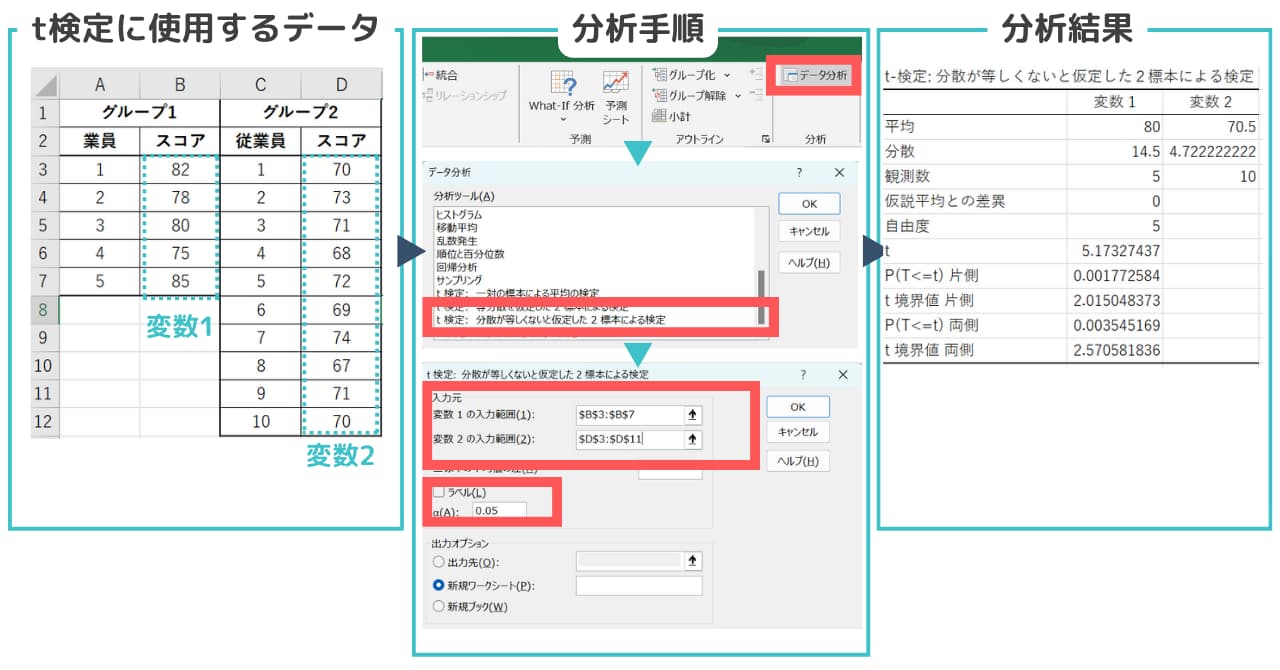
ExcelのT-testには主に3種類あります。T検定は、2つのグループの平均値の差が統計的に有意であるかどうかを判断するために使用される統計手法です。

T検定の種類

T検定には、主に3つの種類があります。これらの検定は、データの特性や分析の目的に応じて使い分けられます。以下に主なT検定の種類を示します。

1. 対応のあるT検定：同じ被験者に対して異なる条件下で測定を行った場合の平均値の比較に使用します。
2. 対応のないT検定：異なる被験者グループ間で平均値を比較する場合に使用します。
3. ウェルチのT検定：対応のないT検定の一種で、2つのグループの分散が等しくない場合に使用します。

T検定の適用条件

T検定を適用する際には、いくつかの条件を確認する必要があります。これらの条件を満たさない場合、検定の結果が信頼できない可能性があります。主な条件としては、データの正規性や分散の等質性などがあります。

1. データが正規分布に従っていること
2. 対応のないT検定の場合、2つのグループの分散が等しいかどうかを確認する必要があります
3. 外れ値がないか、または外れ値の影響が少ないことを確認します

ExcelでのT検定の実行方法

Excelでは、T検定を簡単に行うことができます。具体的には、「データ分析」ツールを使用してT検定を実行します。T.TEST関数を使用することもできますが、「データ分析」ツールを使用すると、より詳細な結果を得ることができます。

1. 「データ」タブの「データ分析」を選択します
2. 「T検定: 対応のある2標本による平均の検定」または「T検定: 対応のない2標本による平均の検定 (分散が等しいと仮定)」、「T検定: 対応のない2標本による平均の検定 (分散が等しくないと仮定)」を選択します
3. 必要な範囲を選択し、有意水準を設定します

カイ二乗検定にはサンプル数はいくつ必要ですか？

カイ二乗検定は、カテゴリカルデータの分析に広く使用されている統計的手法であり、観察された頻度と期待される頻度の間の差が統計的に有意であるかどうかを判断するために使用されます。カイ二乗検定を実施する際、サンプル数の適切なサイズを決定することは、結果の信頼性と有効性を確保する上で非常に重要です。一般的には、カイ二乗検定には十分なサンプル数が必要であり、通常は各カテゴリに最低5つの観察値が含まれることが推奨されています。

サンプルサイズの決定要因

サンプルサイズの決定は、複数の要因によって影響を受けます。まず、効果量の大きさが重要であり、検出したい差が大きいほど必要なサンプルサイズは小さくなります。次に、有意水準（通常は0.05）と検出力（通常は0.8）がサンプルサイズの計算に影響します。また、期待頻度が小さい場合、より多くのサンプルが必要になります。具体的には以下の点が考慮されます。

1. 研究の目的と仮説を明確にし、必要な検出力を決定する
2. 効果量を推定し、必要なサンプルサイズを計算する
3. 期待頻度が小さいカテゴリがある場合は、サンプルサイズを増やす

カイ二乗検定のサンプルサイズ計算

カイ二乗検定のサンプルサイズを計算する際は、GPowerやSASなどの統計ソフトウェアや、オンラインのサンプルサイズ計算ツールを使用することが一般的です。これらのツールを使用することで、研究者は必要なサンプルサイズを簡単に計算できます。サンプルサイズの計算では、自由度、効果量、有意水準、および検出力が重要なパラメータとなります。重要な点は以下の通りです。

1. 効果量の推定には、過去の研究やパイロットスタディの結果を使用する
2. 有意水準と検出力を適切に設定する
3. 自由度を正しく計算し、サンプルサイズの計算に反映させる

サンプルサイズ不足の影響

サンプルサイズが不足している場合、カイ二乗検定の結果は信頼できないものになります。偽陰性のリスクが高まり、有意な差が検出されない可能性があります。また、推定の精度も低下し、結果の一般化可能性が損なわれます。したがって、研究者はサンプルサイズの計画に十分な注意を払う必要があります。サンプルサイズ不足の影響は以下の通りです。

1. 検出力の低下により、真の効果が検出されない
2. 推定の精度が低下し、結果の信頼性が損なわれる
3. 研究の有効性が損なわれ、結果の一般化が困難になる

詳細情報

Excelのカイ二乗検定とは何ですか？

Excelのカイ二乗検定は、2つのカテゴリ変数間に統計的有意な関連性があるかどうかを調べるために使用される統計分析手法です。この検定は、観測された度数と期待される度数を比較して、有意差があるかどうかを判断します。

カイ二乗検定の使い方は？

カイ二乗検定を使用するには、まず2つのカテゴリ変数を含むデータを準備する必要があります。次に、ExcelのCHISQ.TEST関数を使用して、観測された度数と期待される度数を比較します。検定の結果は、p値として表示され、通常は0.05以下の場合に有意と判断されます。

カイ二乗検定の結果をどう解釈するのですか？

カイ二乗検定の結果は、p値に基づいて解釈されます。p値が0.05以下の場合、2つのカテゴリ変数間に統計的有意な関連性があると判断されます。一方、p値が0.05より大きい場合、関連性はないと判断されます。

カイ二乗検定の限界は何ですか？

カイ二乗検定にはいくつかの限界があります。たとえば、サンプルサイズが小さい場合、検定の結果は信頼できない可能性があります。また、カテゴリ変数のカテゴリ数が多い場合、検定の結果を解釈するのが難しくなる可能性があります。したがって、カイ二乗検定を使用する際には、これらの限界を考慮する必要があります。